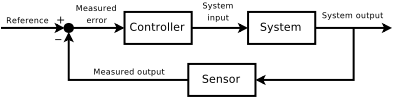
CONTROL THEORY is an interdisciplinary branch of ENGINEERING and MATHEMATICS, that deals with the behavior of DYNAMICAL SYSTEMS. The desired output of a system is called the reference. When one or more output variables of a system need to follow a certain reference over time, a controller manipulates the inputs to a system to obtain the desired effect on the output of the system.

EXAMPLE
Consider a car's cruise control, which is a device designed to maintain a constant vehicle speed with the desired or reference speed provided by the driver. The system in this case is the vehicle. The system output is the vehicle speed, and the control variable is the engine's throttle position which influences engine torque output.

A primitive way to implement cruise control is simply to lock the throttle position when the driver engages cruise control. However, on mountain terrain, the vehicle will slow down going uphill and accelerate going downhill. In fact, any parameter different from what was assumed at design time will translate into a proportional error in the output velocity, including exact mass of the vehicle, wind resistance, and tire pressure. This type of controller is called an OPEN-LOOP CONTROLLER because there is no direct connection between the output of the system (the vehicle's speed) and the actual conditions encountered; that is to say, the system does not and can not compensate for unexpected forces.

In a CLOSED-LOOP CONTROL SYSTEM, a sensor monitors the output (the vehicle's speed) and feeds the data to a computer which continuously adjusts the control input (the throttle) as necessary to keep the control error to a minimum (that is, to maintain the desired speed). Feedback on how the system is actually performing allows the controller (vehicle's on board computer) to dynamically compensate for disturbances to the system, such as changes in slope of the ground or wind speed. An ideal feedback control system cancels out all errors, effectively mitigating the effects of any forces that might or might not arise during operation and producing a response in the system that perfectly matches the user's wishes. In reality, this cannot be achieved due to measurement errors in the sensors, delays in the controller, and imperfections in the control input.

OTHER EXAMPLES - Automatic Pilot (Guidance Systems), Centrifugal Governor, Fire-control Systems

CLASSICAL CONTROL THEORY
To avoid the problems of the open-loop controller, control theory introduces feedback. A closed-loop controller uses feedback to control states or outputs of a DYNAMICAL SYSTEM. Its name comes from the information path in the system: process inputs (e.g. voltage applied to an electric motor) have an effect on the process outputs (e.g. velocity or torque of the motor), which is measured with sensors and processed by the controller; the result (the control signal) is used as input to the process, closing the loop.

CLOSED-LOOP CONTROLLERS have the following advantages over OPEN-LOOP CONTROLLERS:

* disturbance rejection (such as unmeasured friction in a motor)
* guaranteed performance even with model uncertainties, when the model structure does not match perfectly the real process and the model parameters are not exact
* unstable processes can be stabilized
* reduced sensitivity to parameter variations
* improved reference tracking performance

In some systems, closed-loop and open-loop control are used simultaneously. In such systems, the open-loop control is termed FEEDFORWARD and serves to further improve reference tracking performance.

A common CLOSED-LOOP CONTROLLER architecture is the PID CONTROLLER. The PID CONTROLLER is probably the most-used FEEDBACK CONTROL DESIGN. PID is an acronym for PROPORTIONAL-INTEGRAL-DIFFERENTIAL, referring to the three terms operating on the error signal to produce a control signal.

MODERN CONTROL THEORY
In contrast to the FREQUENCY DOMAIN ANALYSIS of the CLASSICAL CONTROL THEORY, MODERN CONTROL THEORY utilizes the TIME-DOMAIN STATE SPACE REPRESENTATION, a mathematical model of a physical system as a set of input, output and state variables related by first-order differential equations. To abstract from the number of inputs, outputs and states, the variables are expressed as vectors and the differential and algebraic equations are written in matrix form (the latter only being possible when the dynamical system is linear). The state space representation (also known as the "TIME-DOMAIN APPROACH") provides a convenient and compact way to model and analyze systems with multiple inputs and outputs. With inputs and outputs, we would otherwise have to write down Laplace transforms to encode all the information about a system. Unlike the frequency domain approach, the use of the state space representation is not limited to systems with linear components and zero initial conditions. "STATE SPACE" refers to the space whose axes are the state variables. The state of the system can be represented as a vector within that space.

CONTROLLABILITY AND OBSERVABILITY
Controllability and observability are main issues in the analysis of a system before deciding the best control strategy to be applied, or whether it is even possible to control or stabilize the system. Controllability is related to the possibility of forcing the system into a particular state by using an appropriate control signal. If a state is not controllable, then no signal will ever be able to control the state. If a state is not controllable, but its dynamics are stable, then the state is termed STABILIZABLE. Observability instead is related to the possibility of "observing", through output measurements, the state of a system. If a state is not observable, the controller will never be able to determine the behaviour of an unobservable state and hence cannot use it to stabilize the system. However, similar to the stabilizability condition above, if a state cannot be observed it might still be detectable.

From a geometrical point of view, looking at the states of each variable of the system to be controlled, every "bad" state of these variables must be controllable and observable to ensure a good behaviour in the closed-loop system. That is, if one of the eigenvalues of the system is not both controllable and observable, this part of the dynamics will remain untouched in the closed-loop system. If such an eigenvalue is not stable, the dynamics of this eigenvalue will be present in the closed-loop system which therefore will be unstable. Unobservable poles are not present in the transfer function realization of a state-space representation, which is why sometimes the latter is preferred in dynamical systems analysis.

Solutions to problems of an UNCONTROLLABLE or UNOBSERVABLE SYSTEM include adding ACTUATORS and SENSORS.

Several different CONTROL STRATEGIES have been devised in the past years. These vary from extremely general ones (PID CONTROLLER), to others devoted to very particular classes of systems (especially ROBOTICS or AIRCRAFT CRUISE CONTROL).

A control problem can have several specifications. Stability, of course, is always present: the controller must ensure that the closed-loop system is stable, regardless of the open-loop stability. A poor choice of controller can even worsen the stability of the open-loop system, which must normally be avoided.

Another typical specification is the rejection of a step disturbance; including an integrator in the open-loop chain (i.e. directly before the system under control) easily achieves this. Other classes of disturbances need different types of sub-systems to be included.

Other "classical" control theory specifications regard the time-response of the closed-loop system: these include the rise time (the time needed by the control system to reach the desired value after a perturbation), peak overshoot (the highest value reached by the response before reaching the desired value) and others (settling time, quarter-decay). Frequency domain specifications are usually related to robustness (see after).

Modern performance assessments use some variation of integrated tracking error (IAE,ISA,CQI).

A control system must always have some ROBUSTNESS PROPERTY. A ROBUST CONTROLLER is such that its properties do not change much if applied to a system slightly different from the mathematical one used for its synthesis. This specification is important: no real physical system truly behaves like the series of differential equations used to represent it mathematically. Typically a SIMPLER MATHEMATICAL MODEL is chosen in order to simplify calculations, otherwise the true system dynamics can be so complicated that a complete model is impossible.

CONSTRAINTS
A particular robustness issue is the requirement for a control system to perform properly in the presence of input and state constraints. In the physical world every signal is limited. It could happen that a controller will send control signals that cannot be followed by the physical system: for example, trying to rotate a valve at excessive speed. This can produce undesired behavior of the closed-loop system, or even break actuators or other subsystems. Specific control techniques are available to solve the problem: MODEL PREDICTIVE CONTROL, and ANTI-WIND UP SYSTEMS. The latter consists of an additional control block that ensures that the control signal never exceeds a given threshold.

SYSTEM CLASSIFICATIONS
* Linear Systems Control
* Nonlinear Systems Control
* Decentralized-Distributed Control

MAIN CONTROL TECHNIQUES-STRATEGIES

ADAPTIVE CONTROL 
Adaptive control uses on-line identification of the process parameters, or modification of controller gains, thereby obtaining strong robustness properties. Adaptive controls were applied for the first time in the Aerospace Industry in the 1950s, and have found particular success in that field.

HIERARCHICAL CONTROL 
A Hierarchical control system is a type of Control System in which a set of devices and governing software is arranged in a HIERARCHICAL TREE. When the links in the tree are implemented by a computer network, then that HIERARCHICAL CONTROL SYSTEM is also a form of NETWORKED CONTROL SYSTEM.

INTELLIGENT CONTROL 
Intelligent control uses various Artificial Intelligence (AI) computing approaches like NEURAL NETWORKS, BAYESIAN PROBABILITY, FUZZY LOGIC, MACHINE LEARNING, EVOLUTIONARY COMPUTATION and GENETIC ALGORITHMS to control a dynamic system.

OPTIMAL CONTROL 
Optimal control is a particular control technique in which the control signal optimizes a certain "cost index": for example, in the case of a Satellite, the Jet Thrusts needed to bring it to desired trajectory that consume the least amount of fuel. Two OPTIMAL CONTROL DESIGN METHODS have been widely used in industrial applications, as it has been shown they can GUARANTEE CLOSED-LOOP STABILITY. These are MODEL PREDICTIVE CONTROL (MPC) and LINEAR-QUADRATIC-GAUSSIAN CONTROL (LQG). The first can more explicitly take into account constraints on the signals in the system, which is an important feature in many industrial processes. However, the "OPTIMAL CONTROL" structure in MPC is only a means to achieve such a result, as it does not optimize a true performance index of the closed-loop control system. Together with PID CONTROLLERS, MPC systems are the most widely used CONTROL TECHNIQUE in PROCESS CONTROL.

ROBUST CONTROL 
Robust control deals explicitly with uncertainty in its approach to controller design. Controllers designed using ROBUST CONTROL METHODS tend to be able to cope with small differences between the TRUE SYSTEM and the NOMINAL MODEL used for design. The early methods of Bode and others were fairly robust; the STATE-SPACE METHODS invented in the 1960s and 1970s were sometimes found to lack robustness. A modern example of a robust control technique is H-INFINITY LOOP-SHAPING. Robust methods aim to achieve robust performance and-or stability in the presence of small modeling errors.

STOCHASTIC CONTROL 
Stochastic control deals with control design with uncertainty in the model. In typical stochastic control problems, it is assumed that there exist RANDOM NOISE and DISTURBANCES in the model and the controller, and the control design must take into account these RANDOM DEVIATIONS.

Call PDQIE to Implement Your State-of-the-Art Process Controls (877) PDQ-4-FIX